Maths

Unequal Probability

In the last session we saw how probability is about chance.

We looked at the following:

• How many chances are there in total and what is your chance of getting your choice?
• Equal probabilities (i.e. the chances of something happening being the same for all)
• Heads and tails both being 1/2 and throwing a number on a dice, each number being 1/6
• All probabilities totalling 1

Today we are going extend the concept of probability and show you 
how to deal with unequal probabilities.

So far we have looked at the chance (probability) of something happening being an equal chance,
i.e. what is the probability of throwing a 4 on a 6-sided dice?
The answer is of course 1/6
Each number has got an EQUAL chance of being thrown.
What is the chance that any number but 3 will come up?

Remember that probabilities must add to one:
So the answer is 5/6. (Because the probability of a 3 coming up is 1/6. So 1/6 + 5/6 = 1).

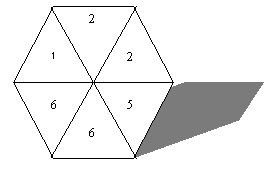
Look at the spinner below:

What is the probability of this spinner landing on a 6?
The answer is 2/6 (six choices and 2 sixes).

What is the chance of getting a 1?
Go to answer

Answer
1/6

Here you can see that the chances of getting a number are NOT equal.
This is unequal probability. However the total probability still adds up to 1

That is almost it for probability. Try these questions on unequal probability.

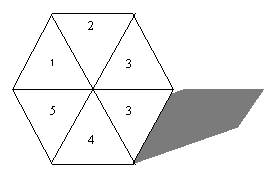
Look at the spinner above. Currently it has landed on 4.

(a) What is the probability of getting 2?
(b) What is the probability of getting 1?
(c) Which number is the spinner more likely to land on?
(d) Pete says that there is an even chance that the spinner will land on an even number. Is he right?

Go to answers

Answers

(a) What is the probability of getting 2? 1/6
(b) What is the probability of getting 1? 1/6
(c) Which number is the spinner more likely to land on? 3; there is a greater probability that the spinner will land on 3 because there are two 3s. So the probability is 2/6 which = 1/3.
(d) Pete says that there is an even chance that the spinner will land on an even number. Is he right? NO he is wrong. There are six numbers and only two ( 2, and 4) are even. The probability of landing on an even number is 2/6 = 1/3, but the probability of landing on an odd number is 4/6 = 2/3.

Well how did you do?

That wasn't too bad was it?
Remember, always read the question carefully
Next time we will look at changing probabilities.
Good Luck

Return to top