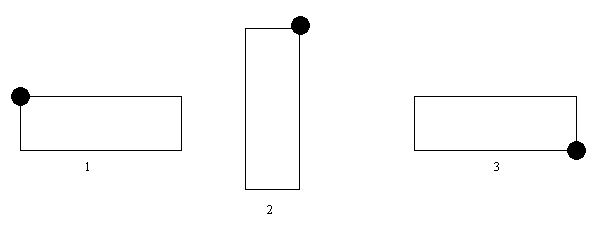
Rotational Symmetry
Symmetry means balance or form.
In maths we often talk about shapes and things being symmetrical.
There are two types of symmetry, line symmetry and rotational symmetry. We have already covered line symmetry. We will cover rotational symmetry today.
Rotational symmetry
If we turn an object round will it look the same?
Here is an example
We have put a blob in one corner to show it turning round.

You see that apart from the blob the shape looks exactly the same in 1 and 3.
We say that this shape has got rotational symmetry of order 2. ( That just means that there are two positions in which it looks exactly the same.
Here is a letter with rotational order of two. Can you see why?

You could turn (rotate) the letter s around to its new position and you would not know
it had changed (we have put the blob on to show you).
What do you think the rotational symmetry order of A is?
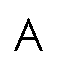
A has got rotational symmetry of order 1
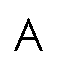
This is just a complicated why of saying that you can not turn A around to any other position so it looks the same.
So rotational symmetry order of 1 means NO rotational symmetry (we can't rotate it).
Try and find out the rotational order of symmetry of the following shapes and letters.
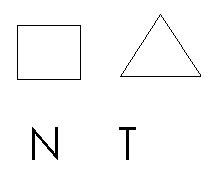
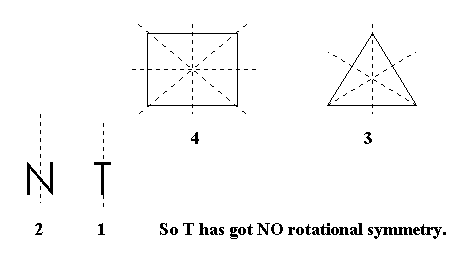
That wasn't too hard was it?
Just to review.
Rotational symmetry is where you can turn an object so that it looks exactly the same. The number of positions
in which it looks exactly the same gives you its order of symmetry.